InCognito

Finite state machines may seem rather mysterious, but odds are that they conform to your intuitions.¹ The challenge, rather, is understanding how to build a finite state machine with well-structured code. So, let's walk through the idea of a simple finite state machine using JavaScript. Discussion in the post will focus on abstract concepts. If you would like to see the code, right-click and inspect the page.

A finite state machine is composed of objects. Each object is a member of a class. Object are related to one another in light of their attributes and rules, defined by class status. The rules govern the nature and path of transitions from the current state. Rules governing transitions interpret data from the environment. To the extent that objects communicate information between one another, objects that communicate in any way can mutually impact the states of one another.

The concept of the the finite state machine can be explained using the example of a binary counter. Binary counting refers to counting in base $2$, as compared to counting in base $10$ where each digit refer to a power of $10$. Counting to four in binary would go as follows. The numbers $1$, $2$, $3$, and $4$, correspond to $1$, $10$, $11$, and $100$. To improve the intuition, we could include all $3$ digits while counting. So just as $02$ refers to the number $2$ in base $10$, $010$ refers to the number $2$ in base $2$. We could represent counting to $4$ in binary as $001$, $010$, $011$, and $100$.

Perhaps you are beginning to see a pattern. Each digit represents the product of the number presented in that digit and the value indicated by the digits place. For example, in base $10$ the number 451 represent the summation: $400$ + $050$ + $001$. This can be represented more granularly as $4(100)$ + $5(10)$ + $1(1)$. Taking this one step further, we can see that this can be rewritten as $4(10^2) + 5(10^1) + 1(10^0)$.

Presenting the place value using exponents of $10$ present us with the pattern that we will use for counting in any other base. Suppose that we wanted to count to $10$ in base $2$. To do this, we will need $4$ bits. Before we count, we can infer that $4$ bits will be needed because the maximum value of $3$ bits can be presented as: $111$. This is equivalent to $1(2^0) + 1(2^1) + 1(2^2) = 1 + 2 + 4 = 7$. If we add 1 more using only 3 bits, we will generate an overflow. This is because $111 + 001 = 1000$. Since there is no fourth bit $(2^3)$, counting starts over at $000$.

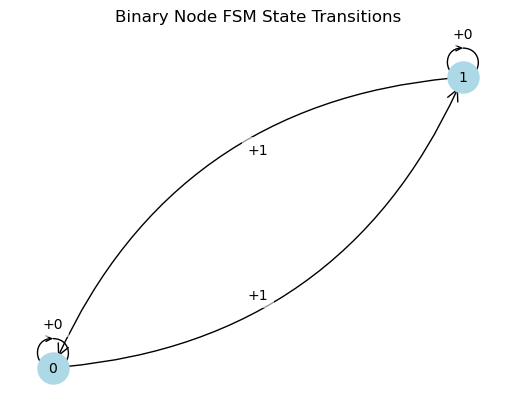
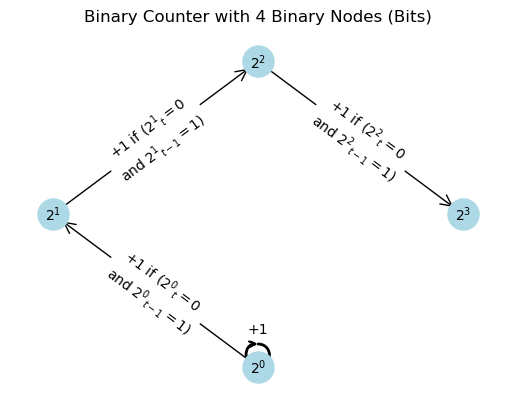
To present binary counting using finite state machines, we can think of each node itself as a finite state machine. When the first node counts up from a value of $1$, the value of node $0$ $(2^0)$ is reset to $0$ and the value $1$ is carried over to node $1$. If node $1$ moves from a value of $1$ to a value of $0$, then a $1$ is carried to node $2$. This pattern continues as long as there are additional nodes to which a carry value can be passed. No matter how many binary nodes are used, if all nodes are set to $1$, then the upward count of node $0$ from $1$ to $0$ will generate an overflow. This incrementing of the first node sets off a chain reaction that will reset all nodes to $0$.

The JavaScript application at the top of this page demonstrates binary counting. But what is more important for our purpose, the script is structured to make a system composed of finite state machines easier to interpret. The application is, itself, a finite state machine. The application is initiated as an instance of the Menu class. The initial MenuState owned by the Menu object is the MainMenuState. This state includes two buttons that transform the MenuState into either the CountingMenuState or the DoSomethingRandomState. The CountingMenuState is linked to the binary counting machine by the Increment button. Clicking the Increment button impacts the value of node $0$. The state of node $0$, in turn, impacts the state of node $1$. The pattern continues, as described in the earlier discussion of binary counting. The state of the finite machine can also be impacted by the Number of Bits slider. The DoSomethingRandomState generates a random number between $1$ and $100$. The value of that number is a consequence of clicking the Generate Number button.

I will reiterate this information with clarification of the class structure. In the script there are two main classes: Menu and BinaryNode. Each of these classes owns a state object. State objects for each of the main classes are constructed as extensions of the abstract state class, unique for each of the main classes. Each abstract state class has some finite number of extensions. The Menu object, for example, can have a MainMenuState, a CountingMenuState, and a DoSomethingRandomMenuStateState.

The CountingMenuState owns a list of BinaryNode objects that are finite state machines used for binary counting. Each BinaryNode object has a state object that is either an ActiveState or an InactiveState. The ActiveState and InactiveState objects are extensions of the abstract NodeState class. The NodeState class has two extensions: ActiveState and InactiveState. Each of the nodes owns a left attribute that identifies which node will receive the carry value when the node is incremented from $1$ to $0$. The Increment button calls the increment method of the first node which is linked to the remaining nodes as I have described. The DoSomethingRandomState is, by comparison, quite simple since it only generates random numbers.

This simple JavaScript application clarifies how object oriented programming can be used to elaborate the structure of finite state machines if the script uses the abstract state classes with extensions of the class that represent particular states that an instance of the class can manifest. Clarification of the structure of finite state machines improves our ability to model complex systems, including well-ordered systems with autonomous, purposive agents. In future posts, I will use this structure to clarify disorganized and organized complexity as conveyed by Warren Weaver (1948).

¹ This discussion is informed by a similar presentation from Marvin Minsky's book Computation: Finite and Infinite Machines. I encourage anyone who would like to better understand finite state machines to spend time with this classic computer science text.