Some of the most powerful tools of modern macro lack micro-foundations.
Given the sort of micro-foundations that have been attempted to this point in
time, I don’t mind that my research employs aggregate demand (AD) as equivalent
to the money stock (M) times velocity (V). In other words, the quantity theory
as an accounting identity is a useful tool for macroeconomic analysis. For
those not familiar, see this simple AD-AS graph.
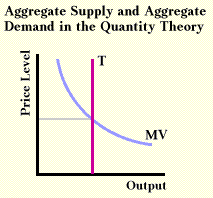
Output measured in nominal terms is P*y. The quantity equation states that P*y =
MV. (This is an accounting identity that provides macroeconomics with its own macro-foundations.) We can replace AD with MV as a result of the accounting identity known as the quantity equation. This presents
an intuitive framework for understanding fluctuations in aggregate demand. If M
rises (falls), then AD rises (falls). Likewise for velocity which is the
inverse of portfolio demand for money – think of portfolio demand (1/V) as cash
reserves as opposed to transactions demand (output, y) which is money spent on goods and services.
We know that, for example, in depressions M and V tend to
move together. The broader stock of money contracts and velocity falls (demand
for money rises). So the quantity theory guides us to consider the composition
of and changes in the money stock. We can ask, why the money stock fell during
the Great Depression and find that waves of bank failures in the United States led
to a monetary contraction. We find that these failures were due to a
combination of a fragile unit-banking system which disallowed large banks from
operating branch banks and tight monetary policy from the Federal Reserve. The
latter was due to a dedication to maintaining high level of gold reserves,
which was part of a general increase in demand for gold by central banks. The
quantity theory tells us that these factors surely pushed down gold denominated
prices and played a significant role in the international crisis.
Research that employs the quantity theory has been fruitful
and I assume that it will continue to be so.
While useful, reliance on economic aggregates also obscure
analysis. These aggregates do not act on one another directly, but emerge
through individual interactions. Causation is not always obvious and requires careful intepretation. Note that I
can rewrite the quantity equation four ways:
M
= P*y/V
V
= P*y/M
P
= M*V/y
y
= M*V/P
One may dig deeper into causation and define each variable
by a set of parameters. Say we define M as a function of output and the interest
rate, M(y, i) and y as a function of capital, labor, and technology, y(K, AL). This
entails greater specificity and a nice model that we can test econometrically. This may provide us with new information, but
we are left operating within a framework that conveys a teleological myth that
says, “given starting point A, the economy will move to point B.” Good
economists work around this problem, but can we have a branch of macroeconomics
that embraces the problem itself?
Richard Wagner thinks so. He observes the problem discussed
above,
Equilibrium-centered macro theory can, of course, give an account
of interdependence among economic activities. Indeed, such an account is
perhaps the prime virtue of this theoretical framework. What it cannot do,
however, is give an account of turbulence that arises through inconsistencies among
plans because no action is presumed to take place until all plans are mutually
consistent. All plans are pre-reconciled within the equilibrium framework, just
as the actions of the members of a parade are pre-reconciled. The alternative
to the equilibrium framework is to treat the ecology of plans as an emergent process
where macro-level objects supervene on micro-level interaction. Any relation
among macro-level variables is thus intermediated through interaction among
entities at the micro level. (“The Macro Economy as an Emergent Ecology of Plans”, 438)
The economy is itself defined by turbulence and this
turbulence cannot be consistently observed via macroeconomic aggregates, though
it does generate the macroeconomic data. To posit the macroeconomy as a formula
with an optimal solution ignores the competition and conflict that occur at the
micro level.
How can one model the sort of competition that I underscored
in yesterday’s post? How can one represent an economy that does not move
directly from equilibrium to equilibrium? Or an economy without equilibrium in
the strict sense? Recent attempts have drawn on string theory where there are
different layers of interaction (
Potts, 2000;
Potts and Morrison, 2007). For
their “micro meso macro” framework, Potts and Morrisson explain,
In mmm [micro meso macro], an economic system is conceptualized as
being made of
generic rules that allow
carriers to perform
operations (
Dopfer
and Potts, 2004).
A rule and its population of carriers is a meso unit, the macroeconomic system
is a complex system of connected meso units, and economic evolution is the
process of change in meso units, either through novel generic rules being
introduced into the economic system or through a change in the population of
each meso rule.
Evolutionary
macroeconomics is the study of how the entire systems of meso are coordinated and
how they change. Evolutionary mesoeconomics is concerned with the structure and
population of each generic rule, and evolutionary microeconomics is the study
of the individual processes of adoption by a carrier (such as an agent) of the
rule. This framework is intended to capture the idea of economic evolution
as a process of endogenous transformation of the economic order through the
origination, adoption and retention of new economic ideas, or generic rules,
that may variously manifest as behaviours, organizing rules or technologies.
(
Potts and Morrison, 309)
Micro meso macro is a convenient representative case of this new macroeconomics. It emphasizes connections between individuals,
resources, firms, etc… and rules about those connections.
The task is far from
complete. The challenge is to build and employ models that impart new understanding
of market processes and the emergence of institutions. These will be models
that include the messy details of individual interaction and of randomness. Within
this framework, one can include optimization as one possible outcome without
being constrained by its determinism and avoid "throwing the baby out with the bathwater."
